In This Section
- Home
- Semester and Timetable Information
- Study Physics
- Our Research
- Our People
- Careers and Alumni
- Seminars, News and Events
- Outreach and School Resources
- About the School
- What is Physics
- The Crawford Observatory
- Frequently Asked Questions
- UCC Futures Quantum & Photonics
- Supports/EDI
The moment of inertia of an object is its resistance to rotational acceleration. This is similar to its mass being its resistance to linear acceleration.Indeed, the rotational inertia of an object depends on its mass. It also depends on the distribution of that mass relative to the axis of rotation.
The relationshiop between the centre of mass and the rotational inertia is explored in this lab. A rigid body as pictured below is used. This is a wooden lamina in which a line of holes have been drilled. The large hole is the wooden lamina makes the distribution of mass around the whole body unequal.
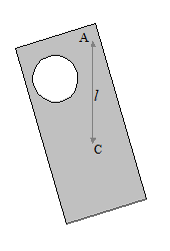
The rigid body is hung from a sensor through the drillled holes. The rigid body can be given a slight push to allow it to start swinging. The sensor which is connected to a computer and the associated software can be used to record and display period of oscillation.
A graph of the period of oscillation (T) and the inverse of distance of each point from the centre of mass (1/l) can be plotted and the slope of the graph calculated. As such using the below equation, and measuring the mass of the rigid body, the moment if Inertia can be calculated.
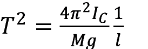
School of Physics
Scoil na Fisice
Contact us
Room 213 (Physics Office), 2nd floor, Kane Science Building, University College Cork, Ireland.,
